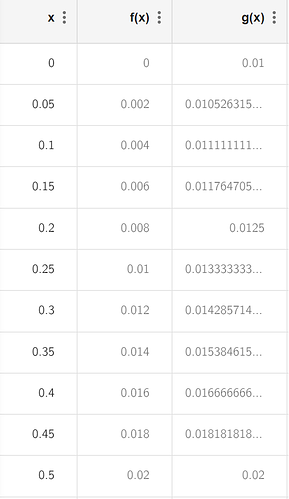
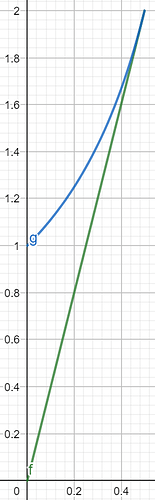
Understood. Let’s consider usage of 2 weapons in the ratio of x and 1 - x (0 < x <= 0,5). If I graph the bonus by x by my and your method, it will look like this:
My method: The bonus is calculated by f(x) = [1 - (0,5 - x)/0,5] x 1% x 2
Your method: The bonus is calculated by g(x) = 1% + [x/(1-x)] x 1%
(x-axis represents the first weapon usage (x), y-axis represents the bonus (%))
As you can see:
+) In your method, the bonus changes hyperbolically from 1% to 2%. The bonus got nerfed slightly in unbalanced case. And, the bonus of your method is always higher than mine.
+) In my method, the bonus changes linearly from near 0% to 2%. If you mainly used weapon for over 75% (the other less than 25%), the bonus will even drop below 1%. This encourage balanced usage of 2 weapons better.
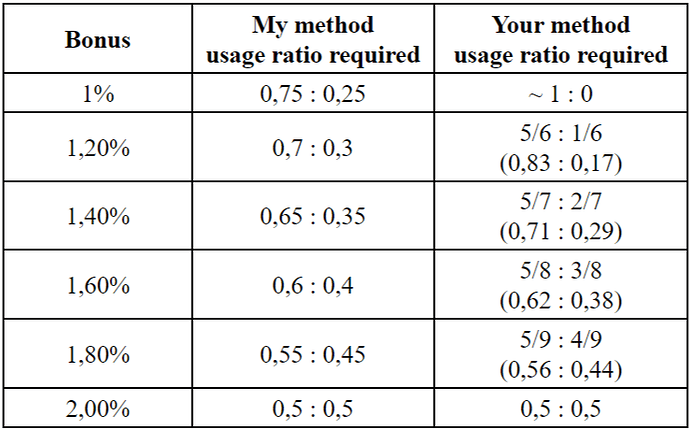
So, to get the same bonus, you need to use 2 weapons more balanced in my method:
Let’s try a more complicated version. Consider weapon usage in the ratio of x : y : (1 - x - y) (suppose x was the most used).
+) In my method, the bonus is calculated by f(x) = (1 - |1/3 - x|/1/3) x 1% + (1 - |1/3 - y|/1/3) x 1% + (1 - |x + y - 2/3|/1/3) x 1%
+) In your method, the bonus is calculated by g(x) = 1% + y/x x 1% + (1 - x - y)/x x 1%
Alright I’m out can’t graph it in 3D
Alright how about 4 weapons? I tried to write out some examples and things get interesting:
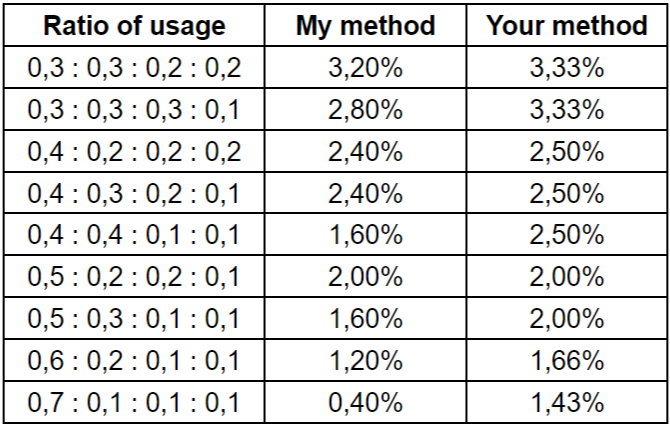
The bonus in your method is always equal or higher than my method.
I noticed that I can simplify your function:
+) Let x be the ratio of most used weapon and n be the number of weapons share the largest ratio (if exist). Your function is simply [n + (1 - nx)/x] x 1%.
+) Now the factors matter is the usage of the most used weapon and the number of weapon used which shared the largest ratio, which is indeed impossible because you can’t perfectly balance them.
+) So, I can safely remove “n” from the function (n = 1), it will be [1 + (1 - x)/x] x 1% which imply that you define usage balance only by the usage of the most used weapon. Then the usage of all other remaining weapons won’t matter.
You can see, in your method, the bonus is the same for 0,5 : 0,2 : 0,2 : 0,1 as well as 0,5 : 0,3 : 0,1 : 0,1 since 0,5 was the only most used. But are these 2 case equally unbalanced? Generally, every ratio 0,5 : x : y : z … (obviously x, y, z… < 0,5) will result in the bonus of 2%, regardless of how unbalanced is x : y : z… and how many weapons else you used. Consider ratio 0,5 : 0,05 (x 10 times), your method will still 2% but mine is 5,5%.
A 0,4 : x : y : z… (x, y, z < 0,4) will always result in 2,5% bonus in your method. If 2, 3, 4, 5, 6 other weapons is equally used besides that 0,4 one; my method will result in the bonus of 2,6%; 2,8%; 3%; 3,2% and 3,4% respectively. I think my method did better in representing balance and also encourage usage of various weapons.
All projectiles now ignore already-killed enemies in their collision checks (allows instant-hit weapons like Laser and Riddler, and to a lesser extent fast-moving ones like Boron and Hypergun, to ‘penetrate’ through enemies)